Mit Bild
Beginnen wir zuerst mit einem Beispiel, warum und wie Sie mit Tabellen-Zellen rechnen, die wechselseitig voneinander abhängig berechnet werden.
Mit Bild
Rekursion zulassen
Damit Excel das nicht mit der anfangs genannten Meldung als fehlerhaft bemängelt, müssen Sie dieses so genannte iterative (schrittweise) Rechnen erlauben.
Mit Bild
Damit fällt auch schon der Hinweis auf die notwendige Begrenzung der schrittweisen Berechnung, denn eigentlich ist eine solche gegenseitige Abhängigkeit endlos: wenn Sie beispielsweise in $B$3 die Formel =C3+1 und in $C$3 die Formel =B3+1 berechnen lassen, schaukelt sich das ewig hoch.
Mit Bild
Daher geben Sie unter Extras/Optionen auf der Registerkarte Berechnung mit der Aktivierung von Iteration gleichzeitig eine Begrenzung für die Maximale Iterationszahl und eine Maximale Änderung an.
Mit Bild
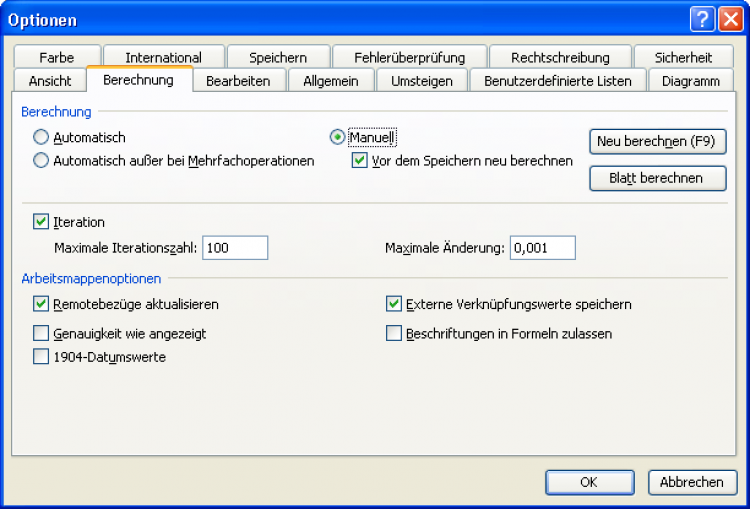
Optionen für Rekursion
Mit Bild
Das gegenseitige Aufschaukeln endet mit den Einstellungen wie im obigen Bild also entweder nach den vorgegebenen 100 Iterationsschritten oder wenn die Differenz zum vorherigen Wert kleiner als die maximale Änderung von 0,001 ist.
Mit Bild
Bitte bedenken Sie dabei, dass diese Einstellung für Excel insgesamt erfolgt, also nicht an die Datei gebunden ist.
Mit Bild
Gegenseitige Abhängigkeiten
Angenommen, Sie wollen wissen, warum es im Winter in jeder Zimmerecke kälter ist als in der Wandmitte und deswegen dort zuerst Schimmel auftritt, bietet es sich an, die Temperaturen einfach für viele Punkte im Raum errechnen zu lassen.
Zur Vereinfachung soll angenommen werden, dass die Temperatur in jeder Zelle der Mittelwert ihrer acht umliegenden Zell-Temperaturen sei. Dazu können Sie die MITTELWERT()-Formel wie im folgenden Bild mit allen 9 Zellen ihres Bereichs benutzen:
Mit Bild
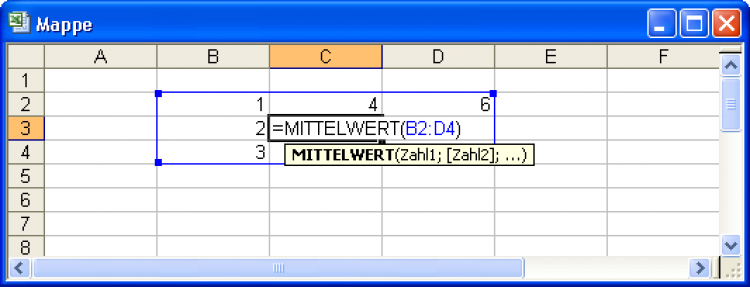
Einfacher Mittelwert aus den umliegenden Zellen
Mit Bild
Im obigen Bild sehen Sie, dass der Mittelwert aus den umliegenden Zellen ohne Weiteres berechnet werden kann.
Mit Bild
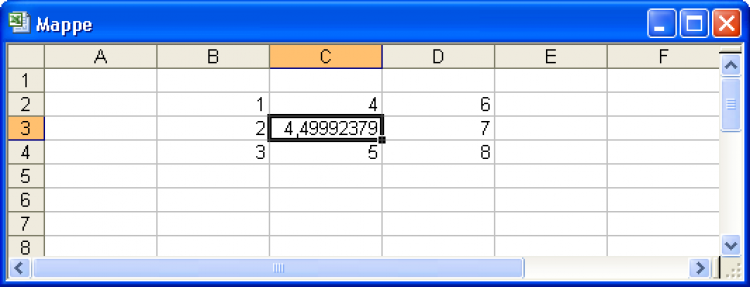
Mit mehrfacher Berechnung (F9-Taste) nähert sich der Mittelwert in $C$3 dem Ergebnis 4,5
Mit Bild
Das ist bereits rekursiv, da die berechnete Zelle $C$3 selber im Daten-Bereich $B$2:$D$4 enthalten ist. Für diese Berechnung ist das noch gar nicht nötig, sondern erhöht nur den Rechenaufwand. Daher sollten Sie die Formel wie folgt verbessern:
Mit Bild
=MITTELWERT(B2:D2;B3:B4;C4:D4;D3)
Mit Bild
Das ist zwar etwas mühsamer in der Eingabe, aber das Ergebnis ist schon im ersten Rechenschritt ohne Rekursion zu ermitteln:
Mit Bild
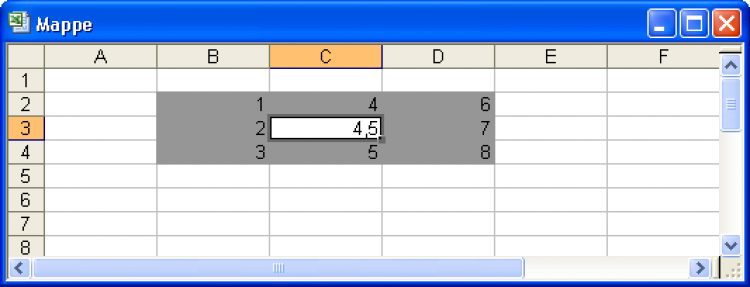
Mittelwert der umliegenden Zellen ohne Rekursion.
Mit Bild
Jetzt ist für diese Formel zwar keine Rekursion mehr nötig, aber die Nachbarzellen enthalten ja keine festen Werte, sondern sind wiederum von ihren umliegenden Zellen abhängig.
Sobald Sie mehrere Temperatur-Zellen im Raum berechnen wollen, sind die Mittelwerte nicht mehr von feststehenden Daten der Nachbarzellen abhängig. Sie greifen vielmehr auf Daten zu, die wechselseitig abhängig sind.
Das ist rekursiv, denn Zelle $B$3 braucht beispielsweise das Ergebnis unter anderem von $C$3, während $C$3 ja sein Ergebnis auch aus $B$3 berechnet.
Mit Bild
Größeres Datenmodell
Jetzt können Sie die Beispielberechnung ein wenig umfangreicher werden lassen. Statt eines einzigen Temperaturwertes im Innern des Raumes sind nun viele möglich.
Markieren Sie beliebige Zellen als "Wand" mit einer angenommenen konstanten Temperatur von 15 Grad Celsius, die hier zudem dunkelgrau markiert wurden. An einer Seite des "Raumes" befindet sich ein Kamin, dessen Feuer konstant 900 Grad heiß ist:
Mit Bild

Temperaturberechnung, noch ohne Berechnung
Mit Bild
Alle Zellen im Inneren enthalten die oben bereits gezeigte Formel für die Berechnung des Mittelwerts, beispielsweise in Zelle $C$4:
Mit Bild
=MITTELWERT(D3:D5;B3:B5;C3;C5)
Mit Bild
Diese Zelle können Sie in alle anderen weißen Zellen hineinkopieren. Sobald Sie die iterative Berechnung in den Optionen aktivieren, errechnet Excel deren Werte wie im folgenden Bild:
Mit Bild
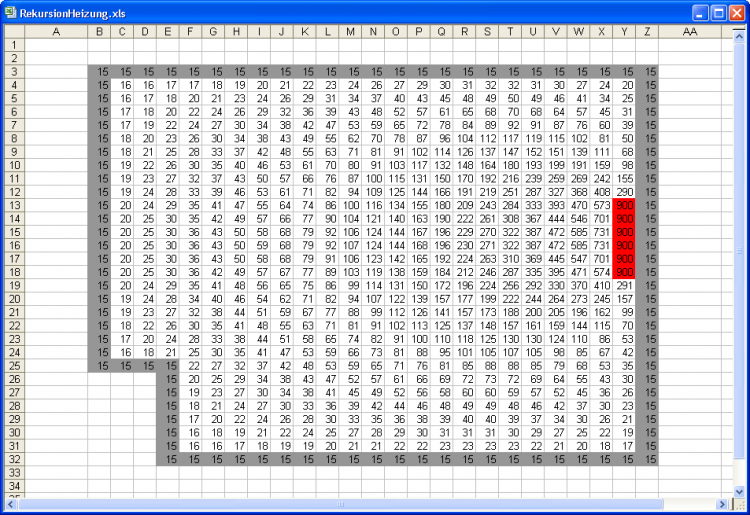
Temperaturberechnung mit rekursiver Formel
Mit Bild
In der Statusleiste können Sie dabei mitverfolgen, wie Excel die Iterationsschritte nacheinander abarbeitet und sich dabei der Lösung nähert. Damit wird natürlich die Menge der berechneten Daten drastisch erhöht. Statt einer einzigen Berechnung pro Zelle muss jede nun bis zu einhundert Mal neu berechnet werden.
Mit Bild
Bedingte Formatierung nutzen
Diese Menge an Zahlen wird bedeutend übersichtlicher, wenn Sie für die weißen Zellen eine Bedingte Formatierung erstellen. Stellen Sie den Dialog mit Format / Bedingte Formatierung wie im folgenden Bild ein:
Mit Bild
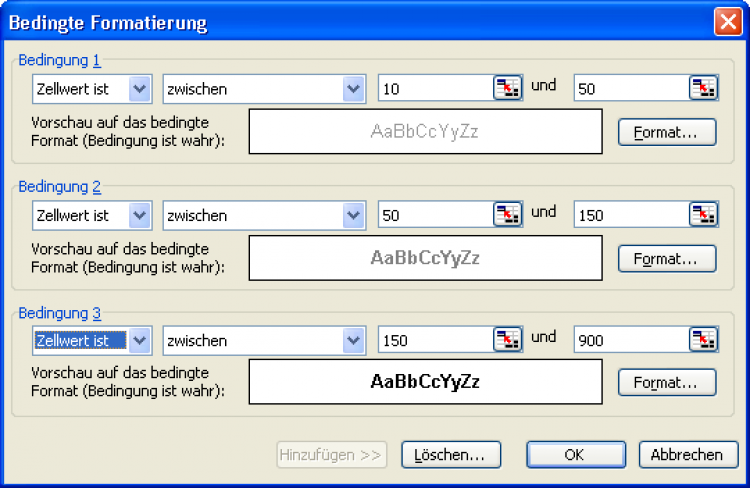
Bedingte Formatierung für die berechneten Zellen
Mit Bild
Anschließend sehen Sie deutlich, wie sich die "Wärme" um den Kamin herum verteilt, weil dort die dunkelsten Zahlen zu sehen sind:
Mit Bild
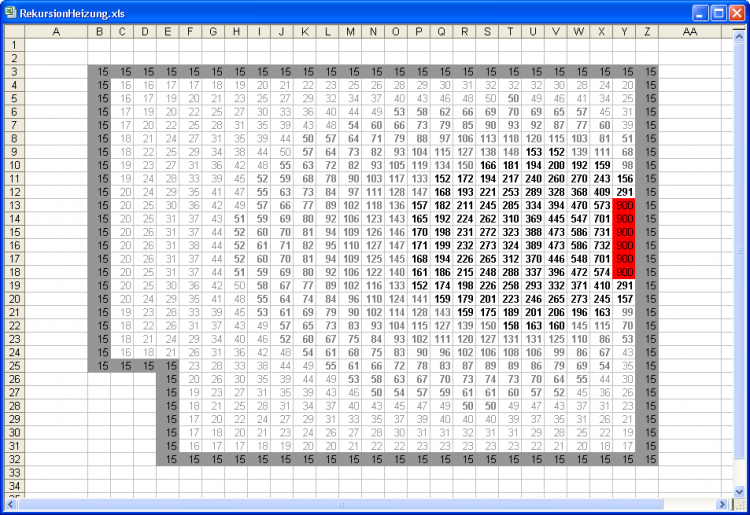
Bedingte Formatierung verdeutlicht die Daten
Mit Bild
Sie können in diesem Rechenmodell sozusagen mal "die Tür aufmachen", indem Sie links unten ein paar Wand-Zellen entfernen und durch berechnete Zellen ersetzen. Damit auch diese wiederum immer konstante Nachbarzellen finden, wurden ein paar fiktive Außenluft-Zellen mit 0 Grad ergänzt:
Mit Bild
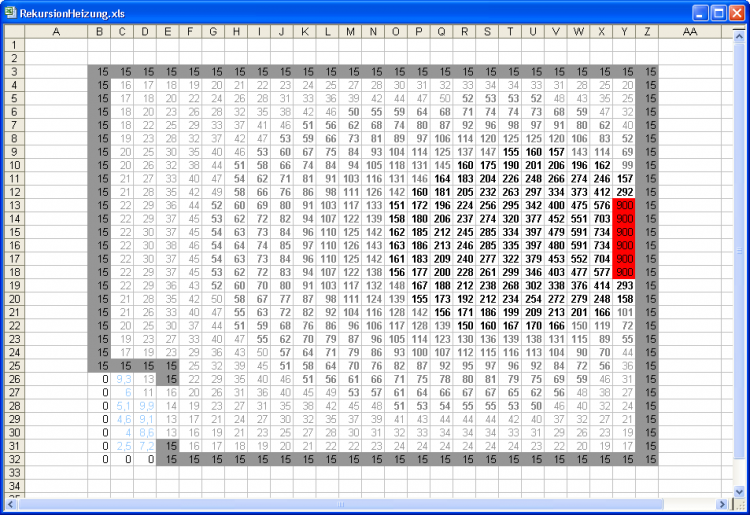
Das Temperatur-Modell mit "geöffneter Tür"
Mit Bild
Hier ist deutlich zu sehen, dass die Raumwärme nach außen entweicht, denn in den hellblau markierten Zellen links unten ist die Temperatur höher als die Außenluft mit ihren 0 Grad Celsius.
Mit Bild
Warum schimmeln vor allem Wand-Ecken?
Um die eingangs gestellte Frage nach dem Schimmel in der Wandecke bauphysikalisch zu beantworten: dort wird die Luft erkennbar gleich von zwei Seiten abgekühlt, ist also deutlich kälter als in Wandmitte.
Da mit niedriger Temperatur immer weniger Wasser von der Luft aufgenommen werden kann, fällt dort Wasser aus, wenn sich die im Rauminnern noch warme Luft hier abkühlt. Passiert das im Luftraum, wird diese Erscheinung landläufig als Nebel bezeichnet.
Auf einer Oberfläche jedoch sammeln sich diese Wassertröpfchen als Kondenswasser (bei schlecht gedämmten Fenstern gut zu beobachten), durchfeuchten die Wand und bilden die ideale Grundlage für Schimmel.
